背景

近日以来，由于学习图像处理，感觉其对傅里叶变换等内容要求较高，故重整旗鼓又过了一遍信号系统等章节，做了不少实验，有所感悟，特记录下，以便备忘！

傅里叶级数

首先，对于傅里叶变换，最为需要理解的便是傅里叶级数，个人感觉这个是后边最为基础也是最为重要的部分，
连续傅里叶级数定义(FS)：

离散傅里叶级数定义(DFS):

从傅里叶级数的定义可以很明显看出，对于一个周期信号，其可以用以一系列的复正弦信号来合成，这一系列信号成谐波关系，另外也可发现对于连续时间信号的合成，需要复正弦信号的“个数”是无穷的，而离散时间信号，需要复正弦信号的“个数”是有限的，为N个，即周期数量多个，这个的原因是由连续和离散信号的特性决定（离散时间复正弦信号周期为2pi）。

傅里叶变换

对于傅里叶变换，其本身看做傅里叶级数的推广（周期为无限长），

连续时间傅里叶变换（FT）：

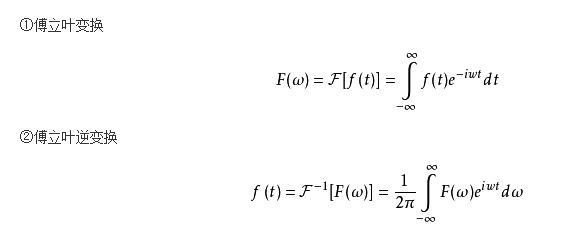
离散时间傅里叶变换（DTFT）：

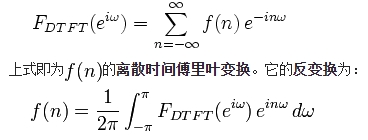
在许多书上，离散时间傅里叶变换都是由是连续信号采样得到的离散信号而得到，这样来介绍，由于有采样频率等的影响，这样会对连续，离散信号产生一定的混淆，个人认为，离散傅里叶变换时离散时间信号的频域特性，并不一定非得和采样，连续信号等产生关系，离散信号可以是由连续信号采样，归一化产生，也可以是其本身就是离散的，如年月日，像素坐标等，如果离散信号是由连续信号采样得到的，那么，当用给定的采样频率，对连续信号采样，归一化后，那么就产生了一个新的离散信号，至于其傅里叶变换和原来的傅里叶变换有何关系，这就是另外一个话题了。

傅里叶变换的核心思想便是能让任意一个信号都可以由一种基本信号来合成，这个基本信号对于

连续时间信号便是:$e^{jwt}$，

离散时间信号便是:$e^{jwn}$。

对于DTFT的定义式，可以发现其积分是由-pi到pi，而对于FT的定义式，积分是从-无穷到+无穷，其根本原因就是，基本信号存在差异，对于exp(jwt)，其不存在周期，当w取任意值，exp(jwt)都会变为一个独一无二的信号，故FT需要从-无穷积分到+无穷，让每一个exp(jwt)都能成为被合成信号的成分（当然这还得取决于前面系数，即傅里叶系数），而对于DTFT而言，由于其基本信号exp(jwn)周期为2pi，故当要合成新信号时，只需要取任何一个2pi区段就可获得合成信号的所有成分，故上式取-pi到pi即可，当然，这样也很容易得出F(exp(jw))也是周期的。

离散傅里叶变换

关于离散傅里叶变换（DFT），其定义为：

可以发现，DFT与离散傅里叶级数（DFS）仅有一点点区别，那就是DFT在逆变换时，即在合成源信号时，会乘上1/N，而DFS相反，除开这一点并无区别，所以这就表示是，DFT实际上是，以信号的N点为周期的信号的离散傅里叶级数，那么DFT和DTFT是什么关系呢？从上述角度上来讲，只能说当DFT所取点数趋于无穷时，那么DFT就可以趋近于DTFT，这也是傅里叶变换的来源，那么书上不是有DFT是DTFT的采样的结论么？该结论是怎样来的？有条件么？

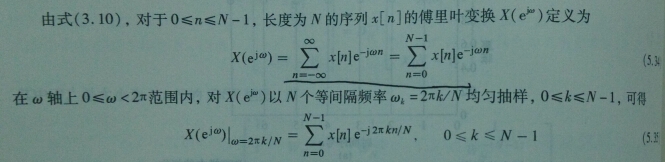
对于上述问题，在图中做了解答，可以发现，只有对于长度为N的有限序列，其取不少于N个点的DFT才是对DTFT的采样，这是由于其序列有限又能有这个结果，个人认为，这也解答了为何DFS与DFT有个系数上的差异，这就是为了在DTFT与DFT的满足采样特点的吻合。另外附上利用DFT模拟DTFT的几张示意图：

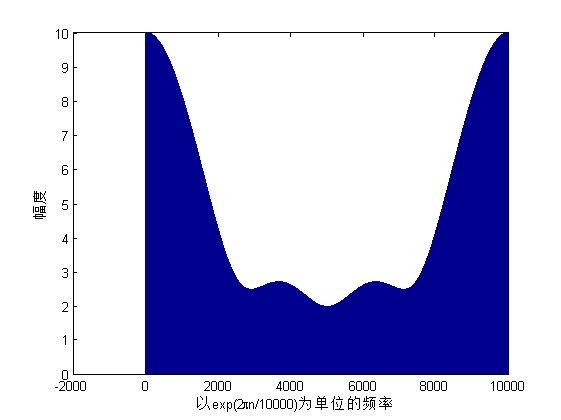
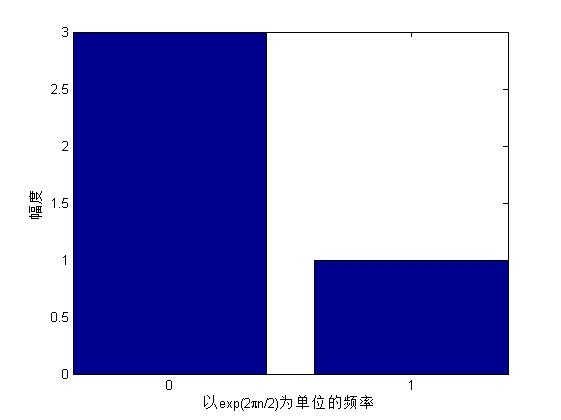
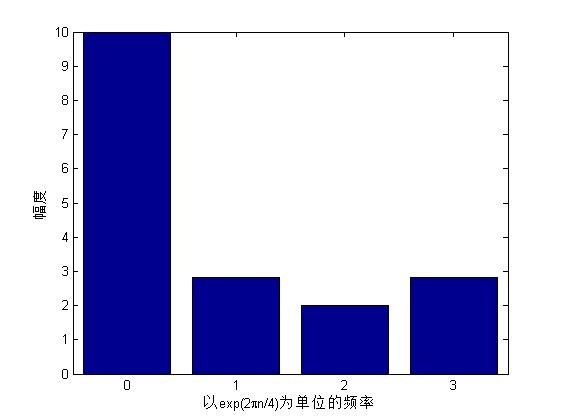
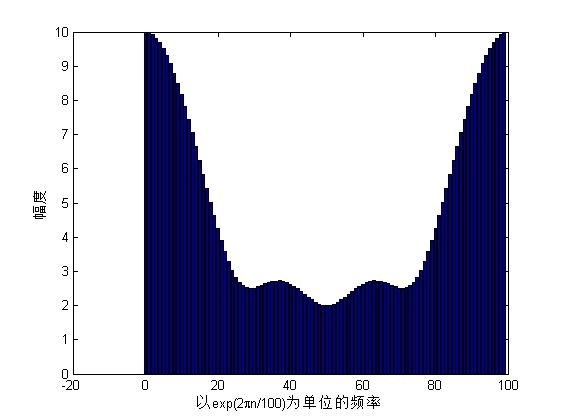
图为序列[1,2,3,4]的各点的dft图

第一幅图取了10000个点，可近似看做dtft，

第二幅图仅仅取了2点，很明显与第一幅图对比，这个并不包含所有信息，故此幅图仅代表[1,2]的两点DFT，

第三幅图取了4点，与第一幅图对比，这个包含所有信息，相当与在dtft中采样出exp(2pi/4)*[0,1,2,3]的值，

第四幅图显然就比较接近与第一幅图了。

本文链接： http://rainlin.top/archives/104
转载请注明转载自： Rainlin Home